感知器，一个线性的判别器，能够实现简单的逻辑运算，比如与非门等；更进一步，引入偏置bias，则在实践中体现便捷；当把感知器整合成神经元，进而通过链式的网络结构，把这些神经元连接，就得到了神经网络，然而神经网络并非如此简单，需要在每个神经元上加入激活函数，不加激活函数便成为完全的线性，与线性回归一致。

在激活函数的变换下，以及网络的结构，发展出很多不同类型的神经网络方法，解决各种不同领域的问题。

感知器

即一个sigmoid神经元，如下图所示，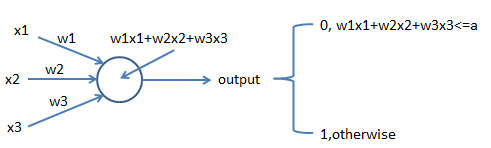

直观地理解，决策前考虑的因素是$x_{j}$，特定因素所对决策的重要性是$w_{j}$。

进一步改进感知器，是引入偏度bias，wx+b，加入b在实践中可以调整。
比较像线性回归，拟合曲线一样，其实线性回归可以用最小二乘法拟合，梯度是另一种求解思路。

激活函数

神经网络需要神经元的激活函数，当权重变化时，则会引起后续神经元变化，从而引起output变化，不断与实际值接近；这样就可以不断调整权重，从而使得预测值与实际值接近。

sigmoid函数是$\sigma (x)=\frac{1}{1+e^{-x}}$,其导数是${\sigma (x)}’=\sigma (x)(1-\sigma (x))$，

当权重和偏置变化时，则会引起输出的变化：$\Delta output\approx \sum_{j}^{N}(\frac{\partial ouput}{\partial w_{j}}\Delta w_{j}+\frac{\partial output}{\partial b}\Delta b)$。

评价w和b的好坏，成本函数最小化，$C(w,b)=\frac{1}{2N}\sum_{x}^{N}\left | y(x)-a \right |^{2}$，

在实践中，我们常用mini_batch的方式来优化w和b，因此，权重和偏置的优化公式分别如下：
$$w_{k}=w_{k}-\frac{\eta }{m}\sum_{j}^{m}\frac{\partial C_{xj}}{\partial w_{k}}$$
$$b_{l}=b_{l}-\frac{\eta }{m}\sum_{j}^{m}\frac{\partial C_{xj}}{\partial b_{l}}$$,

神经网络过程

采取如下表示：
$w_{jk}^{level}$,第level-1层连接到level层，level-1层的第k个神经元连接到底level层的第j个神经元，即目的j源k。

$b_{j}^{level}$，第level层的第j个神经元的bias；

$a_{j}^{level}$，第level层的第j个神经元的激活函数；

$a_{j}^{level}=\sigma (\sum_{k}^{n}w_{jk}^{level}a_{k}^{level-1}+b_{j}^{level})$，上一层所有神经元指向第level层的第j个神经元。

每一层level定义神经元矩阵$w^{level}$，每层的weight矩阵n*m不同，因此，level层的矩阵weight中的第j行k列$w_{jk}^{level}$。

向量计算方式，比如下面简单的例子：
$f(x)=x^{2},f(\begin{bmatrix}2\3\end{bmatrix})=\begin{bmatrix}f(2)\f(3)\end{bmatrix}=\begin{bmatrix}4\9\end{bmatrix}$，因此，神经网络计算可以转为向量的计算$a^{level}=\sigma (w^{level}a^{level-1}+b^{level})$，所以在代码里，会有个中间结果存储$z^{level}=w^{level}a^{level-1}+b^{level}$，

反向传播

如上，则计算单个样本的成本函数是$\frac{1}{2}\sum_{j}^{m}(y_{j}-a_{j}^{L})^{2}$，其中L是最后一层，即输出层；
接着就是把输出层的error反向传播出去，每一层会产生该层的error，不断优化每一层的w和b。
$\xi_{j}^{level}$，表示level层的第j个神经元的error。反向传播的伪代码如下：

1，输入x，设置对应的激活函数a；

2，前向：每一层level计算$z^{level}=w^{level}a^{level-1}+b^{level}$，$a^{level}=\sigma (z^{level})$;

3,输出error，$\xi^{L}=\Delta_{a}C\bigodot{\sigma }’(z^{L})=(a^{L}-y)\bigodot{\sigma }’(z^{L})$;

4,后向传播error，level=L-1,L-2,…,2，计算$\xi^{level}=(w^{level+1}\xi^{level+1}) \bigodot {\sigma }’(z^{level})$；

学习率慢问题

神经网络的学习是成本函数的偏导作为学习率，学习慢意味着偏导很小，那么为什么会很小？因为用sigmoid函数时，偏导一定含有${\sigma }’(x)$，观察sigmoid函数曲线发现，输出接近1时导数接近0，即偏导很小值；

如何解决这一问题，采取方式是交叉熵构造成本函数，是的偏导函数中取决于${\sigma }(x)-y$。

成本函数的构造有不同方式，softmax等，交叉熵等，为的是不同的目标，或者计算过程优化；神经网络过程中的激活函数也有不同作用，像sigmoid会导致梯度越来越小，会使用relu等，tanh等。

线性回归使用L1正则或L2正则，为的是不过拟合